Problemas Resueltos

Auto Evaluación

LIMITES

CONTINUIDAD

continuidad

Se tiene que una función es continua si se puede dibujar “continuamente” sin levantar el lápiz del papel.

Esto se formaliza, a través de las nociones de límites estudiadas hasta ahora, en que una función es continua en un punto a, si cumple: lim┬(x→a)⁡f(x)=f(a)

Observamos que deben cumplirse tres condiciones:

•La función debe estar definida en el punto (debe existir f(a))

•Debe existir el límite de la función en dicho punto.

•Ambos valores deben coincidir.

Si alguna de estas condiciones no se cumple, decimos que la función presenta algún tipo de discontinuidad en el punto.

Esta función es continua en todos sus puntos, porque para todos ellos se tiene que:

lim┬(x→a)⁡f(x)=f(a)

Propiedades y tipos de limites

Tipos de Indeterminaciones

tipos de Indeterminaciones

En los ejemplos anteriores, obteníamos expresiones que tenían sentido en R. Se tenían límites determinados. Si obtuviéramos alguna expresión que no tiene sentido en R, puede ser que el límite fuera 0 o ∞, o bien una indeterminación:

Indeterminación ∞/∞

Empecemos ahora resolviendo cada una de las indeterminaciones anteriores. Comenzamos por las indeterminaciones tipo cociente, y entre ellas, por ∞/∞. Cuando estas indeterminaciones vienen de un límite en el infinito de un cociente de polinomios, dividiremos todos los términos del límite por la potencia de mayor grado:

Indeterminación tipo cociente

Si calculamos un límite en el que hay raíces cuadradas y la indeterminación es ∞/∞, debemos tener en cuenta que el grado del radicando se divide entre dos y que el exponente de x se multiplica por dos al entrar a la raíz:

Si calculamos un límite en el que hay raíces cuadradas y la indeterminación es 0/0, lo que haremos será multiplicar numerador y denominador por el conjugado de la expresión radical:

Indeterminación 0·∞

En estos casos, intentaremos reducir la indeterminación a una del tipo cociente observando que:

En la mayor parte de las situaciones, basta con operar para reducir la indeterminación a una del tipo cociente:

Indeterminación tipo potencia

Casi todas las indeterminaciones tipo potencia se pueden reducir a la indeterminación 1^∞. Para resolverlas necesitaremos conocer un teorema:

Teorema: lim┬(n→∞)⁡〖(1+1/n)^n 〗=e

No damos la demostración del teorema, sino que simplemente observaremos el                                     comportamiento de la sucesión para algunos valores de n:

Se observa que la sucesión es creciente y acotada. El valor del límite es el número                                   e=2,7182818…

Como consecuencia del teorema anterior, se tiene otro similar:Teorema: Si lim┬(x→a)⁡f(x)=∞ entonces lim┬(x→a)⁡〖(1+1/f(x) )^f(x)  〗=e  De este modo, para resolver una indeterminación tipo potencia, el objetivo es convertir la expresión inicial en una del tipo de este teorema:

CONCEPTO Y METODOS DE LIMITES

CONCEPTO DE LIMITE

Un tema central en el estudio del Cálculo es el concepto de límite. A medida que avance el curso se notará que éste concepto aparece en la definición de los conceptos más importantes del  cálculo.  Para  ir  en  búsqueda  de  una  definición  del  límite, exploremos la siguiente situación. En la gráfica a la derecha se observa que los valores que toma una función f(x) en un intervalo abierto (c – δ, c + δ) se va aproximando a un punto denominado c por ambos lados (izquierda y derecha). Así el límite de f(x) es L cuando x tiende a c.

1. MÉTODO NUMÉRICO

Este método permite estimar el límite de una función al evaluar el comportamiento de la misma en varios puntos cercanos a x = c, en dos conjuntos de valores de x, uno que se acerque por su izquierda y otro que se acerque por su derecha para estimar el límite. Veamos los siguientes ejemplos.

EJEMPLO 1: Evalúa la función   F(X)=x2 +1   en varios puntos cercanos a x = 2 y utilizar los resultados para estimar el límite.

Construye una tabla de valores cercanos a x = c, en este caso x = 2. Recuerda asignar valores que se acercan tanto a la izquierda y derecha de c.

x	1.9	1.99	1.999	2	2.001	2.01	2.1
f(x)	4.61	4.9601	4.996001	¿?	5.004001	5.0401	5.41

En la tabla de valores se observa que tanto por la izquierda y por la derecha cuando x = 2  es 5. Entonces se dice que el límite de f(x) cuando x tiende a 2 es 5. En la notación,  lim x→2 f (x ) =5.

EJEMPLO 2: Evalúa la función  F(X ) = x2-7x+10/x-5 en varios puntos cercanos a x = 5 y utilizar 

los resultados para estimar el límite.  

Sustituye cada uno de los valores asignados a x en  f(x ) =   x2-7x+10/x-5        

x	4.9	4.99	4.999	5	5.001	5.01	5.1
f(x)	2.9	2.99	2.999	¿?	3.001	3.01	3.1

 En la tabla de valores se observa que cuando x = 5, se acerca a 3 tanto por la izquierda y  por la derecha. Entonces se dice que el límite de f(x) cuando x tiende a 5 es 3. 

En la  notación, lim  x → 5f (x ) =3     

2.      MÉTODO GRÁFICO

 Este método consiste en analizar la función por medio de su comportamiento gráfico. Los primero que se debe realizar es la construcción de la gráfica de la función. Puedes asignar valores a x para obtener y para dibujar los pares ordenados, utilizar una calculadora gráfica o una calculadora gráfica en línea.

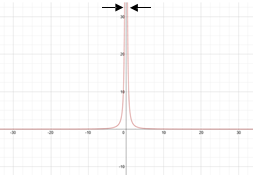
EJEMPLO 1: Evalúa la función  f(x ) = 5/x2   en varios puntos cercanos a x = 0.  

 Empleemos una calculadora gráfica para evaluar el  comportamiento gráfico de la función. En la gráfica se  observa que cuando x tiende a 0 la función sigue  creciendo al infinito. Por lo cual, la función no tiene  límite.

EJEMPLO 2: Evalúa la función f (x ) = x2+1    cuando x tiende a 2.  

 En la gráfica se observa que f(x) se acerca a 5 tanto por la  izquierda como la derecha cuando x tiende a 2. Por lo cual, 

lim     x2 + 1  =5 

x→2    

    EJEMPLO 3: Evalúa la función     lim x→2   f(x )   

                                                        f(x) = {x2+3 ≠2

                                                                     4x=2

Aunque cuando x = 2, existe un punto en (2, 4), al evaluar f(x) tanto por la izquierda como por la derecha tiende a 7. Por lo cual, el límite es 7. O sea,                                               

lim x→2   f(x )=7 

3. MÉTODO ALGEBRAICO 

 Hemos explorado el método numérico y el método gráfico para estimar el límite de una función. En esta sección emplearemos los algoritmos algebraicos para calcular el límite de una función dada. Antes de discutir los ejemplos, estudie las siguientes propiedades de los límites. 

EJEMPLO 1: Determina el límite de la función  f(x ) = 3x2-4x+1         cuando x = 2.   

lim x→2  3x2-4x+1          = lim x →2 3x2 - lim x →2  4x + lim x→2  1  Propiedad de la suma y resta                                                       = 3(2 )2- 4 (2)+1   

                     el limite es =  5

EJEMPLO 2: Encuentra        lim x→-3 =6x3 -9x2

                                           lim x→-3 =  6(-3)3- 9(-3)2

                                           lim x→-3 =  6(-27) - 9(-9)   

                             El límite de f(x) es = -243